Pre-requisite: ম্যাট্রিক্সের ডেফিনিশন, নোটেশন, এসব।
যারা প্রতিযোগিতামূলক খেলাধুলা পছন্দ করে, তাদের পছন্দের একটা বড় অংশ মনে হয় অনেকগুলো দলের মাঝে র্যাংকিং করা। যা অনেক ক্ষেত্রে গিয়ে দাঁড়ায়, নিজের পছন্দের দলের র্যাংক কেমন সেইটা খুঁজে বের করায়।
তো, এইটার ক্ষেত্রে একটা কিঞ্চিত প্যারাডক্সিকাল রেজাল্ট একটু মনে করিয়ে দেই। গত বছরের ফিফা ওয়ার্ল্ডকাপে গ্রুপ ই এর রেজাল্ট ছিল এরকম।
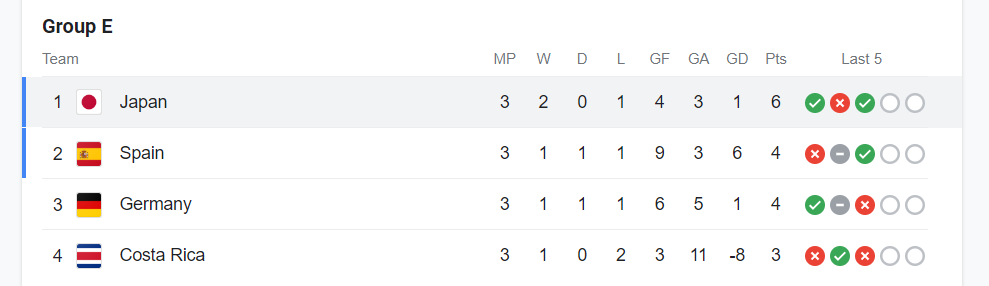
এখানে পয়েন্টের সামারির মধ্যে যেইটা বোঝা যাচ্ছে না, তা হল জাপান হারায় স্পেন আর জার্মানিকে। স্পেন আর জার্মানি নিজেরা ড্র করে, কিন্তু দুই দলই হারায় কোস্টারিকাকে। আর কোস্টারিকার কাছে হেরে বসে জাপান। আমরা সবগুলো ইনফো একটু একটা ছবিতে চিন্তা করি। এখানে 1, 2, 3 আর 4 হল যথাক্রমে জাপান, জার্মানি, স্পেইন, আর কোস্টারিকা। 1 থেকে 2 এর দিকে arrow যাচ্ছে মানে হল গিয়ে 1 এর কাছে 2 হেরে গেছে। (একটু কষ্ট করে মিলিয়ে নিন যে গ্রুপের খেলার রেজাল্ট আর ছবিটা একই কথা বলে। একটাই খেয়াল করার জিনিস, কেউ ড্র করলে আমি তাদের মধ্যে কোন arrow দেই নি)।
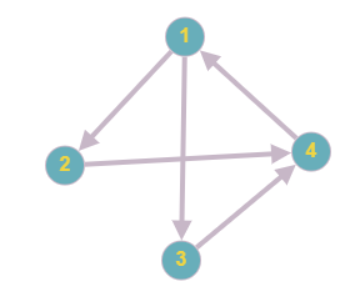
এই একই জিনিসকে ম্যাট্রিক্স দিয়েও প্রকাশ করা যায়। প্রতিটা এলিমেন্ট row team vs column team ম্যাচের রেজাল্ট প্রকাশ করে। জিতলে 1, হারলে 0, ড্র করলে 0.5। একটু মিলিয়ে নিন যে এইটা আর আগের গ্রাফ একই জিনিস (নিজের সাথে নিজের ম্যাচ যেহেতু হয় না, তাই ঐ জায়গায় একটা 0 বসানো)। এই ম্যাট্রিক্সটার নাম দেই M। আমরা ফুটবলের ৩-১-০ পয়েন্ট দিয়ে হিসেব না করে আপাতত এই পয়েন্ট দিয়ে হিসেব করি।

Jargon: এই গ্রাফিকাল রিপ্রেজেন্টেশনকে ম্যাথ/কম্পুসায়েন্সের ভাষায় Directed graph বলে। প্রতিটা টিম একেকটা node, arrow গুলোকে ফরমালি বলে edge বা arc। আর ম্যাট্রিক্স ফর্মটাকে বলে ঐ গ্রাফের adjacency matrix।
এখন, ওয়ার্ল্ডকাপের নিয়ম খুব সোজা, ম্যাচ জিতলে ৩ পয়েন্ট, ড্র করলে ১ পয়েন্ট, হারলে ০। সুতরাং জাপানের পয়েন্ট ৬, জার্মানি আর স্পেনের ৪ করে, প্রশ্নটা দাঁড়ায় এদের মধ্যে কারা যাবে। ফিফার সল্যুশন সবার আগে কে বেশি গোল করে কম গোল খেয়েছে এইটা দেখা, সো স্পেন পরের রাউন্ডে যাচ্ছে।
ইন্টারেস্টিংলি এনাফ, কোস্টারিকার কথা কেউ ভাবছে না। ভাবার কথাও না, সবার নিচে বেচারারা জিতেছে একটা ম্যাচ। কিন্তু কোস্টারিকা চিন্তা করতে পারে অন্যভাবে- “আমরা তো গ্রুপ চ্যাম্পিয়নদের হারিয়েছি। এর কি কোন দাম নাই?”
Well-established tournament rules যেখানে আছে, সেখানে আসলেই কোন দাম নাই। কিন্তু এসিব রুল-টুল তৈরি হওয়ার আগে, এই একই প্রশ্ন উঠেছিল আসলে দাবা খেলার সময়। ধরা যাক, দশজনের একটা টুর্নামেন্ট। সবার সাথে সবার ম্যাচ হবে। দিনশেষে খেলোয়াড়দের র্যাংক করা হবে কিভাবে? সিম্পল উপায় হচ্ছে সব জেতা খেলার জন্য ১ পয়েন্ট দেওয়া, ড্র-এর জন্য হাফ, তারপর যোগ করে ফেলা। একদম ফুটবলের মতই।
কিন্তু সেই ১৮৭৩ সালে, এক অস্ট্রিয়ান প্লেয়ার Oscar Gelbfuhs প্রপোজ করেন একটা রিপিটেড মেথড। ফুটবলের উদাহরণটা যদি দেখি, অস্কারের প্রপোজাল অনুযায়ী রিপিট করা হবে এভাবে, কোস্টারিকা যেহেতু জাপানকে হারিয়েছে, আর জাপান যে বাকি দুই দলকে হারিয়ে দিয়েছে, এর জন্য তারও কিছু পয়েন্ট প্রাপ্য। ইন ফ্যাক্ট, জাপান যত পয়েন্ট পেয়েছে, অত পয়েন্ট কোস্টারিকাকে দিয়ে দেওয়া হোক। আর কাউকে তো সে হারায় নি, তাহলে জাপানের পয়েন্টটাই তার সম্বল। তাহলে কোস্টারিকার নতুন পয়েন্ট কত হবে? জাপানের থেকে পাওয়া 2। একইভাবে সবারই স্কোর আপডেট হয়ে যাবে। এইখানে আসলে পর্দার আড়ালে একটা ম্যাট্রিক্স অপারেশন হচ্ছে। আগে যেই M ছিল, সেই M কে স্কোয়ার করা হয়ে গেছে।

এর পিছনে লজিকটা মূলত এরকম যে, আমি যাকে হারিয়েছি সে যদি অনেক স্ট্রং হয়, তাহলে আসলে আমার তার জন্য বেশি পয়েন্ট পাওয়া উচিত। আবার সে যদি উইক হয়, তার জন্য খুব একটা কিছু না। এইখানে কোস্টারিকার রো-এর দিকে একটু দেখি। এই M-squared ম্যাট্রিক্সে, তার হারানো দল জাপান যে স্পেন আর জার্মানিকে হারিয়েছে, সে জন্য সে স্পেন আর জার্মানিকে হারানোর পয়েন্ট পাচ্ছে। এখন হঠাত করে দেখা যাচ্ছে, নতুন এই ম্যাট্রিক্স হিসেব করলে সবার পয়েন্ট
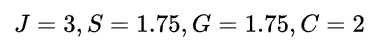
অর্থাৎ হঠাত করে কোস্টারিকার পয়েন্ট বেশি হয়ে গেল। এখন, এইখানে জার্মানি, স্পেন আবার প্রশ্ন তুলতে পারে। আমরা একবার রিপিট করে থেমে যাব কেন? আরেকবার রিপিট করা যাক। অথবা আরও দুইবার। অর্থাৎ M² এর বদলে M³ বা M⁵, ইত্যাদি। ইন্টারেস্টিংলি M⁴ নিয়ে হিসেব করতে গেলে আবার জার্মানি আর স্পেনের পয়েন্ট কোস্টারিকার চেয়ে বেশি হয়ে যাবে।
এই প্রশ্ন দেখে, Edmund Landau কিছুদিন পর নতুন প্রস্তাব দেন: ম্যাট্রিক্স কয়বার গুণ করা ভাল এইসব চিন্তা না করে, আমরা বরং এমন কোন হিসেব করি যা ম্যাট্রিক্সের পাওয়ারের উপর নির্ভরশীল না। তার প্রস্তাবটা অনেকটা এরকম। ধরে নেই, চার দলের চারটা স্কোর আছে, যা একটা ভেক্টর দিয়ে লেখা যায়।
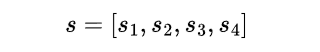
এখন, এই স্কোরটা স্টেবল হবে কখন? যখন “আমি অমুককে হারিয়েছি, সুতরাং তমুকের স্কোর থেকে আমাকে কিছু পয়েন্ট দেওয়া হোক” কথার কোন তাৎপর্য থাকবে না। অর্থাৎ, আমার হারানো লোকজনের ইফেক্ট এড করতে গেলেও স্কোর চেঞ্জ হবে না। এই সম্পর্কটাকে ম্যাট্রিক্স নোটেশন দিয়ে লেখা যায় এভাবে-
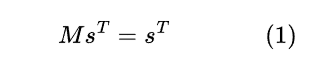
এই (1) রিলেশনটার সমাধান থাকা আবার সবসময় সম্ভব না। অর্থাৎ এরকম s থাকবে, এইটা সব ম্যাট্রিক্স M এর জন্য নিশ্চিত না। কিন্তু, আমাদের উদ্দেশ্য যদি শুধু একজন আরেকজনের রিলেটিভ স্কোর বের করাই হয়, তাহলে এর খুব কাছাকাছি আরেকটা রিলেশন বের করা সম্ভব, যা সব সময়ে সত্যি হবে। সেইটা দেখতে কেমন?
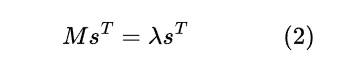
এখানে λ হচ্ছে যেকোন পজিটিভ রিয়েল নাম্বার (একটা কন্সট্যান্ট পজিটিভ নাম্বার দিয়ে গুন করা হলে আসলে আমাদের স্কোরের খুব বেশি কিছু যায় আসে না। 10,8,6,4 আর 5,4,3,2 তো র্যাংক বের করার স্বার্থে একই কাজ করে, তাই না?)। এই নতুন (2) রিলেশনটার আবার সবসময় সল্যুশন পাওয়া সম্ভব। M ম্যাট্রিক্সের সব সংখ্যা যদি জিরো বা পজিটিভ নাম্বার হয়, তাহলে এইটার সব সময় সমাধান থাকবে। আর আমাদের ক্ষেত্রে তো অবশ্যই জয়ের সংখ্যা, ড্রয়ের সংখ্যা পজিটিভ। এই রেজাল্টটা সাধারণত Perron-Frobenius Theorem(PFT) নামে পরিচিত। আমরা এর প্রুফ-টুফে যাব না, সত্যি বলে মেনে নিব আপাতত।
যারা একটু-আকটু লিনিয়ার এলজেব্রা পারেন, তারা খেয়াল করে থাকবেন, বাকিদের জন্য বলে রাখি। এই λ হচ্ছে ম্যাট্রিক্স M এর right eigenvalue। আমি একটু হ্যান্ড-ওয়েভ করে সল্যুশন থাকবে বলে দিচ্ছি। কিন্তু PFT আসলে বলে যে অবশ্যই এরকম ম্যাট্রিক্সের একটা পজিটিভ eigenvalue থাকবে, এবং তার সাথে একটা corresponding eigenvector থাকবে যার প্রতিটা মান পজিটিভ। এর নাম leading eigenvector এবং এটাই হবে আমাদের চাওয়া s এর সল্যুশন।
অর্থাৎ, আমরা এখন একটা স্কোর বের করতে পারব, যেইটা আমি যাদের হারাচ্ছি তাদের ইফেক্টটা হিসেবে নিতে পারে। তাহলে আমরা আমাদের ম্যাট্রিক্স M এর জন্য স্কোরগুলো বের করে ফেলি। সমাধান করলে আমরা পাই-
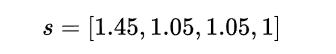
এই স্কোর দেখে অবশেষে মনে হয় জার্মানি আর স্পেন দল হাঁফ ছেড়ে বাঁচতে পারবে। এট লিস্ট কোস্টারিকা থেকে তো বেশি।
এইখানে যদিও মাত্র একটা করে ম্যাচ হয়েছে, এইটা দিয়ে হিসবে করাটা একটু উইয়ার্ড লাগতে পারে। কিন্তু যখন অনেক অনেক ম্যাচ হয়, আর এই “এক হারালো দুইকে, দুই হারালো তিনকে, তিন আবার এককে” ধরণের সাইকেলের সংখ্যা বেড়ে যায়, তখন এরকম কমপ্লেক্স নিয়ম বেশ কাজে লাগে। অনেক ম্যাচ আছে, এরকম এক্সাম্পল বের না করে আমরা আসলে এই ফুটবলের এক্সাম্পলটাতেই আরেকটু ঘাটি। বেশিরভাগ ম্যাচেই তো বিভিন্ন দল গোল-টোল দেয়। তাহলে, আমরা শুধু, জয়-হার না দেখে, খেলার গ্রাফ বা ম্যাট্রিক্সটা বানাই গোলের কাউন্ট দিয়ে। তাহলে আমরা পাই নতুন ম্যাট্রিক্স P।
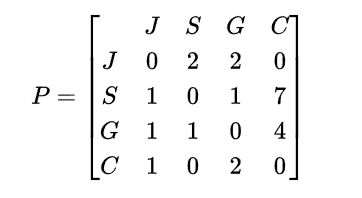
এইটার জন্য আরেকবার leading eigenvector বের করে স্কোর নির্ণয় করা যাক।
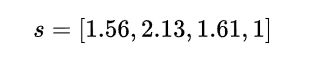
এবার দেখা যায় স্পেন আর জার্মানির স্কোর জাপান থেকেও বেশি। এইটা অবশ্য একদিক দিয়ে ভাবলে ঠিকই আছে। ম্যাট্রিক্স দেকেহ মনে হচ্ছে স্পেন, জার্মানি ৭ বার, ৪ বার হারাচ্ছে কোস্টারিকা কে। জাপানের সাথেও ওরা বেশ ইভেন, ২ বার হারে তো ১ বার হারায়। খুব unintuitive result তা বলা যাবে না। এবং এই এক্সাম্পলটা আগের সিম্পলটার থেকে বেশি দেখায় কেন এরকম অদ্ভুত সব র্যাঙ্কিং মেথড দরকার। কারণ একেকজন একেক সংখ্যক ম্যাচ খেলছে।
এরকম র্যাংকিং বের করার বেশ অনেক নিয়ম আবিষ্কার হয়েছে এই গত দেড়শ-দুইশব বছরে দাবা, ক্রিকেট, যাই হোক, সেই ক্ষেত্রে ব্যবহার করার জন্য। Learning to rank নামে এই ফিল্ড তৈরি হয়েছে এসব কাজের জন্য, এবং এই টপিকে রিসার্চ এখনও চলে, থিওরেটিকাল ম্যাথ থেকে শুরু করে মেশিন লার্নিং এর লোকজনের হাতে।
আজকের আলোচনা করা মেথডটা Spectral ranking নামের একটা বেশ সাধারণ মেথডের স্পেশাল কেইস বলা যায়। Learning to rank এর সবচেয়ে well-known এলগিরদম সম্ভবত PageRank, যার উপর দাঁড়িয়ে ছিল Google এর আদি ব্যবসা। কোন কোন দিক দিয়ে PageRank কেও আসলে স্পেক্ট্রাল র্যাঙ্কিং মেথড বলা যায়।
স্পেক্ট্রাল র্যাংকিং নিয়ে আইডিয়া পেতে এই সার্ভে পেপারটা খুব ভাল (আমি যা বলেছি তা মোটামুটি প্রথম দুই পেইজে আলোচনা করে ফেলে এই পেপারে)-
Vigna, Sebastiano. “Spectral ranking.” Network Science 4.4 (2016): 433–445.